Der Begriff der Menge ist elementar und wird daher nicht definiert. Bekanntlich kann eine Menge durch Aufzählung ihrer Elemente, und evtl. nur dadurch, bestimmt sein. Solcherart heterogene Mengen spielen freilich fast nirgends eine Rolle. Normalerweise hat man mit Mengen zu tun, deren Elemente etwas miteinander gemeinsam haben. Eine solche Menge ist eine Klasse.
Mi ist eine Klasse von Mj, genau dann wenn Mi eine Klasse ist und in Mj inkludiert ist. (Normalerweise ist auch Mj eine Klasse; aber das ist nicht notwendig.) In diesem Sinne sind z.B. Säugetiere eine Klasse von Tieren, und Rauhhaardackel sind sowohl eine Klasse von Tieren als auch eine von Säugetieren.
Ein Merkmal ist eine kennzeichnende, unterscheidende Eigenschaft, d.h. eine Eigenschaft, die die Mitglieder einer Klasse als solche kennzeichnet und von denen einer anderen Klasse unterscheidet. Z.B. ist ‘weiß’ ein unterscheidendes Merkmal von Schimmeln und folglich ein Bestandteil der Intension des Begriffs ‘Schimmel’. Ein Merkmal von Schimmel ist ‘maskulin’.
Sei M eine Menge von Elementen und KM eine Menge von Klassen Ki, derart daß jedes Ki eine Klasse in M ist. M zu klassifizieren heißt, eine solche Menge KM anzugeben. Z.B. kann man eine Menge von Individuen klassifizieren, dadurch daß man sie in Schüler, Studenten, Rentner, Frauen und Behinderte einteilt. Klassifikation heißt sowohl die Operation des Klassifizierens als auch ihr Ergebnis (hier: KM).
Sei Ki eine Klasse in Kj und seien Bi und Bj die den beiden Klassen entsprechenden Begriffe. Dann ist Bi ein Hyponym von Bj.
Eine vollständige Klassifikation von M ist eine solche, für die folgende zwei Bedingungen gelten:
Die beiden Bedingungen werden auch so formuliert: die Klassen einer vollständigen Klassifikation sind
Eine Klassifikation von Fahrzeugen in Land-, Luft- und Wasserfahrzeuge ist nicht vollständig, denn die Klassen sind zwar gemeinsam exhaustiv, aber nicht mutuell exklusiv, weil Amphibienfahrzeuge in zwei Klassen fallen. Wenn die o.a. Klassifikation von Individuen auf die Klasse der Erfurter Bürger angewandt wird, erfüllt sie keine der beiden Bedingungen, weil z.B. Studentinnen in zwei Klassen und gesunde männliche Bankangestellte in keine der Klassen fallen. Dagegen ist die Klassifikation der Artikel der deutschen Sprache in definite und indefinite vollständig.
Eine vollständige Klassifikation wird dadurch erreicht, daß man ein Prinzip angibt, nach dem sich die Intensionen der Klassen unterscheiden. Ein solches Prinzip ist im einfachsten Falle ein Parameter, von dem die Intensionen der Klassen die Werte sind. D.h., es ist eine Eigenschaft, in welcher sich die Elemente klassenweise unterscheiden. Wenn man z.B. eine Menge von Personen nach Altersgruppen klassifiziert, so ist das Alter (im generischen Sinne) der Klassifikationsparameter und jedes einzelne Alter (oder Altersspanne) ein Wert auf diesem Parameter. Ein Parameter in dieser Funktion ist ein Kriterium der Klassifikation.
Im Zusammenhang mit einer Klassifikation ist der Ausdruck Merkmal polysem in dem Sinne, daß er “Parameter”oder “Wert” bedeuten kann. Dasselbe gilt für den Ausdruck Kriterium: sowohl B1.a als auch b sind vernünftige Rede.
| B1. | a. | Als Kriterium zur Klassifikation dieser Gruppe dient das Geschlecht. |
| b. | Das Kriterium der Zuweisung von Erna zu dieser Klasse ist, daß sie weiblich ist. |
Wo nicht anders angegeben, bedeutet Kriterium im folgenden “Klassifikationsparameter”.
Zu jeder Klassifikation sind die Kriterien explizit anzugeben. Die o.a. Klassifikation von Individuen ist auch deswegen nichtig, weil ihre Kriterien nicht angegeben sind. Bei der graphischen Darstellung einer Klassifikation in Form von Matrizen, Bäumen u.ä. sind die Kriterien und Werte obligatorischer Bestandteil der Darstellung.
Die Werte eines Parameters einer vollständigen Klassifikation sind komplementäre Begriffe: wenn einer auf ein Objekt zutrifft, treffen alle anderen nicht zu. (Ist diese Bedingung nicht erfüllt, sind die Klassen nicht mutuell exklusiv.) Hat der Parameter gerade zwei Werte (ist er binär), so sind seine Werte kontradiktorisch. Z.B. sind die Werte der Klassen der beweglichen und der nicht-beweglichen Güter nach einem binären Kriterium mit kontradiktorischen Werten gewonnen. Wenn die Werte eines Kriteriums komplementär (und insbesondere kontradiktorisch) sind, ist die mutuelle Exklusivität der Klassen garantiert.
Eine Klassifikation, die sich aus einem einzigen Kriterium ergibt, ist eindimensional. Sie läßt sich auf mehrere Weisen darstellen, z.B. als Baum wie in folgendem Schema, wo die Elemente a, b, c klassifiziert werden.
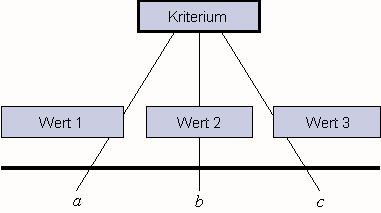
Eine eindimensionale Klassifikation kann man auch in einer eindimensionalen Matrix darstellen, wie in folgendem Beispiel, wo Sitzmöbelbezeichnungen klassifiziert werden und wo das Kriterium das Genus und die Werte die drei Genera sind:
| Genus | maskulinum | femininum | neutrum |
| Elemente | Stuhl, Sessel ... | Couch, Chaiselongue ... | Sofa, Kanapee ... |
|---|
Sobald mehr als ein Kriterium im Spiel ist, ergibt sich eine mehrdimensionale Klassifikation. Hiervon gibt es zwei Haupttypen, nach welchen in den folgenden Schaubildern die Elemente a, b, c, d klassifiziert sind.
Gegeben ist eine Menge von Elementen, z.B. von Bauklötzen verschiedener Formen und Farben. Man kann sie nach unterschiedlichen Kriterien klassifizieren. Eine Klassifikation ergibt sich, wenn man die Form als Kriterium wählt, eine andere, wenn die Farbe das Kriterium ist. Jede der beiden Klassifikationen ist vollständig und eindimensional. Kombiniert man die beiden zu einer einzigen Klassifikation, wird es eine (vollständige) mehrdimensionale, und zwar eine Kreuzklassifikation. Bei einer Kreuzklassifikation sind alle Klassifikationskriterien auf alle Objekte anwendbar. Sie sind nicht voneinander abhängig. Daher ist die Reihenfolge der Anwendung auch gleichgültig. Die folgende Darstellung verdeutlicht das Prinzip:
Kriterium 1 Kriterium 2 ╲ |
Wert 1.1 | Wert 1.2 |
| Wert 2.1 | a | b |
|---|---|---|
| Wert 2.2 | c | d |
Ein einfaches Beispiel ist die erwähnte Klassifikation einer Menge von Bausteinen sowohl nach Form (Kriterium 1) als auch nach Farbe (Kriterium 2). Ein weiteres ist die Klassifikation der Morpheme in lexikalische vs. grammatische sowie in selbständige und gebundene.
Eine Kreuzklassifikation nach zwei Kriterien wird als zweidimensionale Matrix dargestellt. Die Kriterien werden in die linke obere Zelle eingetragen, die Werte in die Zeilen- und Spalteneingänge. Sind mehr als zwei Kriterien miteinander zu “multiplizieren”, so werden mehrdimensionale Darstellungen nötig.
Wenn die Bedingungen für eine Kreuzklassifikation nicht erfüllt sind, ergibt sich eine hierarchische Klassifikation. Das ist vor allem dann der Fall, wenn die Klassifikationskriterien verschieden allgemein sind. Jedes Klassifikationskriterium ist dann nur innerhalb einer Klasse anwendbar, die durch ein allgemeineres Kriterium vorab gebildet ist. Das folgende Schema veranschaulicht das Prinzip.
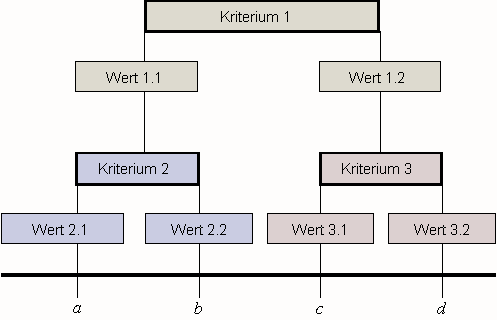
Als Beispiel dieses Schemas kann eine bibliographische Klassifikation von Publikationen dienen:
Kriterium 1: Selbständigkeit der Publikation:
Wert 1.1: selbständig:
Wert 1.2: unselbständig:
Komplexere Beispiele für hierarchische Klassifikationen sind zoologische und botanische Taxonomien. Taxonomien und Meronymien sind Formen der hierarchischen Klassifikation. Somit sind sie mehrdimensionale Klassifikationen. Das erstaunt zunächst, denn zumindest bei einigen Taxonomien und Meronymien waltet tatsächlich ein einziges Kriterium. Z.B. bei einer genetischen Klassifikation von Sprachen lautet es ‘x stammt von y ab’. Das Kriterium ist jedoch keine Eigenschaft, die in gleicher Weise auf alle Individuen anwendbar wäre, so daß sich eine eindimensionale Klassifikation ergäbe, und auch keine Menge solcher Eigenschaften, wodurch sich eine Kreuzklassifikation ergäbe. Es ist vielmehr eine Relation, in welcher der Bezugspunkt y je nach gegebenem x wechselt. Wenn in der genetischen Klassifikation von Sprachen in der Relation ‘x stammt von y ab’ x = Russisch ist, so ist y = Urslavisch; ist x jedoch = Deutsch, so ist y = Urgermanisch. Münzt man also die Relation um in eine Eigenschaft, so lautet sie für Russisch und die anderen slavischen Sprachen ‘stammt von Urslavisch ab’, für Deutsch und die anderen germanischen Sprachen jedoch ‘stammt von Urgermanisch ab’. Hält man also an der Definitionsbedingung fest, daß Klassifikationskriterien Eigenschaften sind, ist eine solche Taxonomie in der Tat eine hierarchische Klassifikation, in welcher die Kriterien nur innerhalb gegebener Klassen gelten.
Eine hierarchische Klassifikation wird als Baum dargestellt; die Verzweigungen werden mit den Kriterien und Werten indiziert. Auch die Kapitel- und Abschnitteinteilung eines Sachbuchs, etwa einer Magisterarbeit, ist i.w.S. eine hierarchische Klassifikation. Daher hat auch sie eine Baumstruktur, die durch die dezimale Gliederung bezeichnet wird.
Viele Klassifikationen sind gemischt. Z.B. die Klassifikation der Sprachlaute durch phonetische Merkmale ist z.T. eine Kreuzklassifikation, etwa ihre Klassifikation nach Lippenrundung ([± rund]) und Konfiguration des Larynx ([± stimmmhaft]). Z.T. ist sie eine hierarchische Klassifikation: Die Merkmale Nasalität ([± nasal]) und Artikulationsstelle ([± suprapharyngal]) hängen voneinander ab, denn Nasalität ([+ nasal]) gibt es nur bei [+ suprapharyngalen] Lauten; und ebenso hängen die Merkmale des Öffnungsgrads von Vokalen ([± offen]) und Stimmhaftigkeit voneinander ab, weil offene Vokale stimmhaft sind.
Der Zweck einer Klassifikation ist es, Ordnung in einen Gegenstandsbereich zu bringen, um ihn kontrollieren zu können. Für diverse praktische Zwecke können die Klassifikationskriterien völlig äußerlich und kontingent sein. Z.B. ist es für bestimmte administrative Zwecke notwendig, Menschen in Führerscheinbesitzer und Nicht-Führerscheinbesitzer einzuteilen. In der Wissenschaft klassifiziert man i.a. nicht zu praktischen Zwecken, sondern um einen Gegenstandsbereich nach allgemeinen Prinzipien kognitiv zu bewältigen. Die Klassifikationskriterien sollen sich aus dem Wesen des Gegenstands ergeben, die Klassifikation soll seiner weiteren Erkenntnis dienen. Diese Bedingungen erfüllt z.B. die Klassifikation von Homo sapiens in Homo sapiens sapiens und Homo sapiens neanderthalensis.