Wie wir schon wiederholt festgestellt hatten, bestehen komplexe Syntagmen, insbes. Sätze, aus Wörtern, die durch syntagmatische Relationen zusammengehalten werden. Hinter der eindimensionalen Abfolge der Wörter oder Morpheme in der Kette ist also eine mindestens zweidimensionale Struktur zu entdecken. Gewisse Teile hängen untereinander enger zusammen als andere; es besteht also eine Hierarchie. Aufgabe einer jeden syntaktischen Analyse ist es, diese hierarchische Struktur explizit zu machen. Die oben eingeführten syntaktischen Kategorien bilden die Voraussetzung für eine Reihe von Modellen der syntaktischen Beschreibung, denen wir uns im folgenden zuwenden. Gegenstand dieses Kapitels ist die Analyse in unmittelbare Konstituenten (engl. immediate constituent analysis, daher auch ‘IC-Analyse’). Die Grundidee dieser Analyse ist dieselbe wie in der strukturalen morphologischen Analyse.
Der IC-Analyse liegt die Inklusionsrelation zwischen verschieden umfassenden Syntagmen zugrunde. Z.B. inkludiert das Syntagma in B1.a u.a. das Syntagma in B1.b, und dieses wieder das Syntagma in c.
| B1. | a. | arbeitete die ganze Nacht |
| b. | die ganze Nacht | |
| c. | ganze Nacht |
Wenn man nun einen beliebig komplexen Ausdruck, z.B. einen ganzen Satz, zu analysieren hat, kann man ihn in zwei Syntagmen zerlegen, aus denen er besteht. Die so gewonnenen Syntagmen kann man wieder zerlegen; und so immer fort, bis man bei den Worteinheiten angelangt ist, die man nach syntaktischen Gesichtspunkten nicht mehr zerlegen kann. Das Verfahren ist dasselbe, das in Kap. 2.2 für die Segmentierung komplexer Wortformen eingeführt worden war. Es wird hier an einem Beispielsatz vorgeführt.
| Ludwig | fährt | den | Wagen | in | die | Garage |
| Ludwig | fährt | den | Wagen | in | die | Garage |
| Ludwig | fährt | den | Wagen | in | die | Garage |
| Ludwig | fährt | den | Wagen | in | die | Garage |
| Ludwig | fährt | den | Wagen | in | die | Garage |
| Ludwig | fährt | den | Wagen | in | die | Garage |
Auf jeder Ebene wird ein binärer Schnitt gelegt (auf der letzten Ebene sind hier zwei gleichartige Schnitte zusammengefaßt), der ein (bereits von senkrechten Strichen begrenztes) Syntagma in zwei Teilsyntagmen zerlegt. Die Schnitte müssen so gelegt werden, daß jeweils Syntagmen i.w.S. abgetrennt werden. Die Entscheidungen werden methodisch kontrolliert durch Substitutions- und Permutationsproben. Die Konstanthaltung des Kontextes einschließlich der syntagmatischen Relationen wird dabei, wie in Kap. 2.1 erläutert, vorausgesetzt.
Das Syntagma Y ist eine Konstituente des Syntagmas X genau dann, wenn Y in X inkludiert ist. Mithin ist das Syntagma in B1.b eine Konstituente des Syntagmas in a, und das in B1.c ist eine Konstituente sowohl des Syntagmas in a als auch desjenigen in b.
Y ist eine unmittelbare Konstituente von X genau dann, wenn Y eine Konstituente von X ist und es kein Z derart gibt, daß Y Konstituente von Z und Z Konstituente von X ist. Folglich ist das Syntagma in B1.b eine unmittelbare Konstituente desjenigen in a, und das in c ist eine unmittelbare Konstituente desjenigen in b, aber nicht desjenigen in a. Jeder der Schnitte im obigen Beispielsatz zerlegt ein Syntagma (das bereits Konstituente eines umfassenderen Syntagmas sein kann) in zwei unmittelbare Konstituenten.
V und W sind Kokonstituenten genau dann, wenn beide unmittelbare Konstituenten von U sind. Z.B. sind in und die Garage im vorigen Schema Kokonstituenten, nicht aber Ludwig und die Garage.
Die Konstituenz oder Konstituentenstruktur eines Syntagmas ist sein Aufbau aus Konstituenten. Das obige Schema zeigt also die Konstituenz des Satzes Ludwig fährt den Wagen in die Garage.
Es gibt eine Reihe von alternativen Verfahren, die Konstituenz zu repräsentieren. Obiges Schema zeigt das Schichtendiagramm. Dieses veranschaulicht lediglich den methodischen Gang und ist sonst zur syntaktischen Repräsentation ungebräuchlich. Daneben gibt es das hier folgende Strukturbaumdiagramm (kurz Strukturbaum, Baumdiagramm oder schlicht "Baum") und die darunter gezeigte Notation mit eckigen Klammern.
| Ludwig | fährt | den | Wagen | in | die | Garage | ||||||||||||
| [ [Ludwig] [ [ [fährt] [ [den] [Wagen] ] ] [ [in] [ [die] [Garage] ] ] ] ] |
Die beiden letzten Diagramme unterscheiden sich vom obigen Schichtendiagramm nur dadurch, daß sie die – theoretisch nicht interessante – methodische Reihenfolge nicht darstellen. Die beiden letzten Diagramme sind in dem, was sie darstellen, genau äquivalent. Man sagt, sie sind notationelle Varianten voneinander. Die Wahl zwischen den beiden Darstellungsweisen unterliegt praktischen Erwägungen (bessere Übersichtlichkeit, aber auch größerer Herstellungsaufwand und Platzbedarf der Baumdarstellung).
| 1. | Konstituentenanalyse durch Permutation |
| 2. | Konstituentenstruktur eines Satzes |
| 3. | Pränominale Modifikatoren |
Bisher haben wir die Darstellung der syntaktischen Struktur als Konstituenz nur als eine Analysemethode kennengelernt. Sie kann jedoch auch für die Grammatiktheorie nutzbar gemacht werden; denn sie erlaubt es, den hierarchischen Aufbau eines syntaktisch komplexen sprachlichen Zeichens in Regeln zu fassen. Dazu benötigen wir die im vorigen Kapitel eingeführten syntaktischen Kategorien und Wortarten (und einige mehr, falls die Theorie vollständig sein soll). Konstituenz wird ja nicht ad hoc für eine gegebene Kette festgelegt, sondern sie gilt für Syntagmen, insoweit sie und die sie konstituierenden Syntagmen bestimmten Distributionsklassen oder syntaktischen Kategorien angehören. Deshalb setzt eine explizite Konstituentenstrukturanalyse die Zuweisung der Wörter zu Wortarten voraus.
Wir hatten bereits gesehen, daß eine syntaktische Kategorie im konkreten Fall durch ein Syntagma aus Mitgliedern anderer syntaktischer Kategorien oder auch einfach durch ein Mitglied einer geeigneten Wortart repräsentiert sein kann. Die Kombinationsmöglichkeiten von Syntagmen bestimmter Kategorien zu umfassenderen Syntagmen sind nun begrenzt. D.h. wir können empirisch feststellen, daß es im Hinblick auf die Kategorien der Konstituenten nur eine endliche (meist kleine) Anzahl von Möglichkeiten der Konstituenz für ein Syntagma einer gegebenen Kategorie gibt. Diese können wir wie folgt aufzählen.
| 1. | S | = | NSNom + VS |
| 2. | NS | = | S |
| 3. | NS | = | Det + Nom |
| 4. | NS | = | Pron |
| 5. | NS | = | Nprop |
| 6. | Nom | = | Adj-al + Nom |
| 7. | Nom | = | Nom + NSGen |
| 8. | Nom | = | Nom + S |
| 9. | Nom | = | Ncom |
| 10. | Adj-al | = | Adv-al + Adj-al |
| 11. | Adj-al | = | Adj |
| 12. | VS | = | VS + Adv-al |
| 13. | VS | = | Vtr + NSAkk |
| 14. | VS | = | Vitr |
| 15. | Adv-al | = | Adv-al + Adv-al |
| 16. | Adv-al | = | PräpS |
| 17. | Adv-al | = | SAdv |
| 18. | Adv-al | = | Adv |
| 19. | PräpS | = | Präp + NSobl |
| 20. | SAdv | = | Konj + S |
Die Tatsache, daß die Tabelle die Regel 16 und daneben keine andere enthält, die auf der rechten Seite ausschließlich ein PräpS hätte, besagt, daß jedes PräpS ein Adv-al ist. Zum Begriff des Adverbials s.o.
Die in der Regelmenge zusätzlich eingeführten Abkürzungen sind wie folgt zu lesen:
| NSNom | NS im Nominativ | Vtr | transitives Verb | |
| NSGen | NS im Genitiv | Vitr | intransitives Verb | |
| NSAkk | NS im Akkusativ | SAdv | Adverbialsatz | |
| NSobl | NS in obliquem Kasus | |||
| Ncom | Nomen commune | |||
| Nprop | Nomen poprium |
Die Kasusindizes sind für die deutsche Syntax notwendig; in einer Konstituentenstrukturgrammatik des Englischen (für das dieses Modell am meisten verwendet wurde) treten sie nicht auf.
Eine Konstituentenstrukturregel ist eine Regel, die für eine Konstituente einer gegebenen syntaktischen Kategorie angibt, welchen Kategorien ihre unmittelbaren Konstituenten angehören. Sie hat folgende allgemeine Form:
A = B + C
A, B und C heißen Kategorialsymbole, da sie ja syntaktische Kategorien symbolisieren. Dabei ist A eine Kategorie einer höheren syntaktischen Ebene, B und C sind syntaktische Kategorien niedrigerer Ebenen. Das Gleichheitszeichen (öfters auch ein Pfeil) steht für die Relation der Konstituenz. Die Regel kann von links nach rechts gelesen werden: "expandiere (erweitere) A zu B plus C" bzw. "ersetze A durch B plus C"; oder von rechts nach links: "eine Kette, die aus B plus C besteht, bildet ein Syntagma der Kategorie A". Regeln dieser Form heißen deshalb auch Expansionsregeln oder Ersetzungsregeln.
Runde Klammern bedeuten hier, wie auch sonst in syntaktischen Repräsentationen, Optionalität (= Fakultativität) des so eingeschlossenen Elements. Die Reihenfolge der durch '+' verknüpften Elemente ist signifikant; d.h. sie entspricht der Reihenfolge, die die entsprechenden Syntagmen in einer aktuellen Kette tatsächlich haben. Gegeben die Form von Regel 1, könnten wir also zwar den Satz Friedrich kommt, nicht aber den Satz Kommt Friedrich? mit den Regeln 1 - 20 beschreiben.
Wenn man die Regeln von links nach rechts liest, geben sie eine formal-syntaktische Rechtfertigung einer Analyseprozedur wie der IC-Analyse. Man könnte ein solches Schichtendiagramm auch von unten nach oben lesen. D.h., gegeben einen bereits in Wörter zerlegten Text, kann man fragen, zu welchen umfassenderen syntaktischen Einheiten die Wörter sich gruppieren. Diese Frage beantwortet man mithilfe der Regelmenge 1 - 20, indem man die Regeln von rechts nach links liest.
Wie alle Konstrukte eines Modells einer empirischen Wissenschaft werden auch Konstituentenstrukturregeln aufgrund empirischer Untersuchungen gewonnen oder getestet. Man legt z.B. ein Korpus deutscher Texte zugrunde und stellt fest, welche Kategorien und Konstituenzverhältnisse man annehmen muß, um alle vorkommenden Strukturen beschreiben zu können. Dabei würde man übrigens sofort feststellen, daß obige Menge für deutsche Texte bei weitem nicht ausreicht. Z.B. ist nicht einmal eine Regel für indirekte Objekte vorgesehen. Doch auf Vollständigkeit soll es hier nicht ankommen.
Ein Regelapparat wie der obige hat aber nicht ein rein methodisches Interesse. Wenn er einmal steht, kann man die Regeln auch in folgendem Sinne von links nach rechts lesen: Man kann sie in abstracto, d.h. ohne eine vorgegebene sprachliche Kette, dazu verwenden, um syntaktische Strukturen aufzubauen. Dieser Prozeß heißt die Generierung (Erzeugung) syntaktischer Strukturen. Wenn man z.B. beliebige Satzstrukturen des Deutschen erzeugen will, muß man mit dem Symbol S anfangen und dieses expandieren. Die dadurch eingeführten Kategorialsymbole muß man weiter expandieren, und so immer fort, bis man nur noch Symbole hat, die nicht auf der linken Seite irgendeiner Regel vorkommen. Dies sind die sogenannten präterminalen Symbole. Ihre Rolle spielen in der Syntax die Wortarten. Die Ableitung einer syntaktischen Struktur (d.h. ihr Aufbau durch schrittweise Anwendung einer Menge von Regeln) ist also beendet, wenn am Fuß des Strukturbaums nur Wortarten stehen.
Wenn ein Regelapparat zwei oder mehr Regeln enthält, die auf der linken Seite dasselbe Symbol haben – wie das in unserer Menge von Konstituentenstrukturregeln wiederholt der Fall ist –, so ist dies so zu verstehen, daß man auf einer gegebenen Stufe der Ableitung das Symbol nach Belieben nach einer der betreffenden Regeln expandieren kann. Solche Regeln sind disjunktiv geordnet. Man verwendet für diese Auswahl auch die Notation mit geschweiften Klammern:
| a. | A = A = | B + C D + E | ||
| b. | A = | { | B + C D + E | } |
Die Fassungen a und b sind Notationsvarianten.
Eine mögliche Anwendung unserer Konstituentenstrukturregelmenge wäre z.B. die folgende (das jeweils neue Resultat ist gelb markiert):
| Anwendung | Resultat |
| Start : | S |
| Regel 1 : | NSNom + VS |
| Regel 5 : | Nprop + VS |
| Regel 12 : | Nprop + VS + Adv-al |
| Regel 13 : | Nprop + Vtr.fin + NSAkk + Adv-al |
| Regel 3: | Nprop + Vtr.fin + Det + Nom + Adv-al |
| Regel 9: | Nprop + Vtr.fin + Det + Ncom + Adv-al |
| Regel 16 : | Nprop + Vtr.fin Det + Ncom + PräpS |
| Regel 19 : | Nprop + Vtr.fin Det + Ncom + Präp + NSobl |
| Regel 3 : | Nprop + Vtr.fin Det + Ncom + Präp + Det + Nom |
| Regel 9 : | Nprop + Vtr.fin Det + N + Präp + Det + Ncom |
Dadurch haben wir nun zufällig die Struktur des Baumdiagramms aus Abschnitt 1 generiert. Die letzte Zeile der Tabelle zeigt die Wortartstruktur des Beispielsatzes, die vorangehenden Zeilen dienen zur Konstruktion des zugehörigen Strukturbaums. Wir brauchen jetzt nur noch eine Konvention, nach welcher die präterminalen Symbole durch je ein Mitglied der betreffenden Wortart repräsentiert werden; dann können wir nicht nur abstrakte Strukturen, sondern Sätze nebst ihren Strukturen wie eben den obigen generieren. Eine solche Konvention kann selbst wieder sehr komplex sein, weil nicht jedes Wort in jede syntaktische Umgebung paßt. Wir übergehen diese Problematik hier und nehmen an, daß am Schluß eines solchen Generierungsprozesses eine terminale Kette, d.i. eine Folge von Wortformen, steht.
Die Generierung von Sätzen nach einem vorgegebenen Regelapparat mag verschiedene praktische Anwendungen haben, z.B. in der Mensch-Maschine-Kommunikation oder im Fremdsprachenunterricht. Für die Syntaxtheorie hat das "Laufenlassen" des Apparats eine eminente methodische Bedeutung. Zur Erzeugung von Sätzen der Sprache gelten nämlich nur die angegebenen Regeln zusammen mit den übrigen Informationen, die zu den diversen Formeln und Symbolen explizit gegeben werden. D.h. der Regelapparat soll nicht mit Verstand und unter Zuhilfenahme muttersprachlicher Intuition, sondern mechanisch angewandt werden. Kommen dabei nur mögliche ("grammatische") Sätze der betreffenden Sprache heraus und können zudem alle Sätze, die in der Sprache möglich sind, auch tatsächlich erzeugt werden, so haben wir ihre syntaktischen Regeln richtig formuliert; d.h. wir haben eine vollständige und präzise Syntax der Sprache verfaßt. Die Anwendung der Regeln dient also, innerhalb der deskriptiven Linguistik, der Kontrolle der Grammatiktheorie.
Die oben angegebene Menge von 20 Regeln ist, wie gesagt, unvollständig. Aber selbst wenn wir die Menge vervollständigten, könnten Erzeugungsregeln nicht alle Satzstrukturen einer Sprache beschreiben. Z.B. haben wir durch die Regeln 2 und 8 die Möglichkeit vorgesehen, Substantivsätze und Relativsätze einzubetten. Aber der Regelapparat kann nicht dafür sorgen, daß ein Satz, wenn er auf eine bestimmte Weise eingebettet ist, mit daß beginnt, und wenn er auf andere Weise eingebettet ist, mit einem Relativpronomen beginnt. Das liegt daran, daß Konstituentenstrukturregeln als kontextfrei konzipiert sind. (In jeder Regel der obigen Menge von Konstituentenstrukturregeln wird das Symbol links des Gleichheitszeichen durch die Kette rechts davon ersetzt, ohne darauf zu achten, was links und rechts des ersetzten Symbols steht.) In einer bestimmten Variante der generativen Grammatik war deshalb vorgesehen, Konstituentenstrukturregeln durch Transformationsregeln zu ergänzen. Diese werden später besprochen.
Das Modell der generativen Grammatik, welches eine solche Konstituentenstrukturgrammatik mit einem Apparat von Transformationsregeln kombinierte, wurde in den 60er und 70er Jahren des 20. Jh. benutzt. Die Konstituentenstrukturgrammatik wird hier – und die Transformation später – einigermaßen ausführlich besprochen, obwohl dieses Modell nicht mehr benutzt wird. Die Besprechung dient auch nicht der Einführung in die generative Transformationsgrammatik. Sie dient erstens dazu, Grundbegriffe der Konstituentenstruktur einzuführen, die bis heute von den meisten Linguisten – völlig unabhängig von jenem Modell – benutzt werden, und zweitens dazu, eine elementare Vorstellung davon zu vermitteln, wie man die grammatische Beschreibung einer Sprache formalisieren kann.
Nachdem wir nun gesehen haben, daß der Beispielsatz nebst Baumdiagramm durch Anwendung von Konstituentenstrukturregeln gewonnen werden kann, ist es nur noch ein kleiner Schritt zu größerer Explizitheit, in dem Baumdiagramm die syntaktischen Kategorien anzugeben, die in dem Ableitungsprozeß expandiert werden. Ein Knoten in einem Strukturbaum ist ein Punkt, an dem die Verzweigung einer umfassenderen Konstituente in zwei (oder mehr) Subkonstituenten dargestellt wird. Die Knoten werden nun mit den Kategorialsymbolen indiziert; d.h. die Kategorialsymbole werden an die Knoten geschrieben. Wir erhalten dann etwa den folgenden Baum als explizitere Fassung des vorigen.
| S | ||||||||||||||||||
| NSNom | VS | |||||||||||||||||
| VS | Adv-al | |||||||||||||||||
| PräpS | ||||||||||||||||||
| NSAkk | NSAkk | |||||||||||||||||
| Nprop.Nom | Vtr.fin | DetAkk | Ncom.Akk | Präp | DetAkk | Ncom.Akk | ||||||||||||
| Ludwig | fährt | den | Wagen | in | die | Garage | ||||||||||||
Stattdessen können wir auch die Klammern indizieren:
Der Knoten X in einem Strukturbaum dominiert den Knoten Y genau dann (unmittelbar), wenn Y eine (unmittelbare) Konstituente von X ist. Z.B. dominiert in obigem Baum der Knoten PräpS die Knoten Präp und NS sowie alle von diesen dominierte Knoten.
In dem Regelformat dürfen auch B oder C = A sein; d.h. auch die folgende Form ist erlaubt:
A = B + A
In unserer Konstituentenstrukturregelmenge gibt es mehrere Fälle dieser allgemeinen Form, und zwar die Regeln 3, 6, 8, 10, 12, 15. Sie haben gemeinsam, daß das Symbol links des Gleichheitszeichens rechts noch einmal auftritt. Für die Anwendung der Regelmenge gilt lediglich die Konvention, daß im Laufe einer Ableitung eine Regel angewendet werden kann, wenn auf der betreffenden Stufe das Kategorialsymbol erreicht ist, das auf ihrer linken Seite steht (und daß der Regelapparat auch weiter angewendet werden muß, solange noch Kategorialsymbole expandiert werden können). D.h. in welcher Reihenfolge die Regeln angewendet werden, ergibt sich aus dem jeweils erreichten Stand der Ableitung, wobei man zwischen disjunktiv geordneten Regeln die Wahl hat. Folglich kann man die soeben aufgezählten Regeln auf ihr eigenes Resultat anwenden. Der Vorgang heißt Rekursion (wörtl. “Zurücklaufen”), und diese Eigenschaft der betreffenden Regeln heißt Rekursivität. B2 zeigt ein paar Beispiele.
| B2. | a. | lief [Adv-al geradezu [Adv-al erstaunlich [Adv-al schnell]]] |
| b. | die [Nom überkandidelte [Nom sympathische [Nom alte [Nom Jungfer]]]] | |
| c. | der Sohn [NSGen des Bruders [NSGen des Hausmeisters [NSGen des Direktors [NSGen der Konservenfabrik]]]] |
Die meisten durch Rekursion zustandekommenden Strukturen – hier die durch Regel 6, 8, 10, 12 und 15 erzeugten Strukturen – haben eine Eigenschaft gemeinsam, die man Endozentrizität nennt. Ein Syntagma ist endozentrisch genau dann, wenn es derselben Kategorie angehört wie seine zentrale Konstituente (andernfalls ist es exozentrisch). Mit der zentralen Konstituente ist die nicht-optionale Konstituente des Syntagmas gemeint, auf die sich das Syntagma bei Streichung der Erweiterungen reduziert. Der Begriff wird in Kap. 2.3.3 unter Zugrundelegung des Dependenzbegriffs als 'Kopf einer Dependenzrelation' expliziert werden. In B2 sind a und b endozentrisch.1
Die Rekursion der genannten Regeln ist direkt, nämlich jeweils in einer einzigen Regel realisiert. Es gibt auch indirekte Rekursion, wenn nämlich die Regeln Ri bis Rn die in folgendem Schema dargestellte formale Beziehung zueinander haben:
| Ri: | A = B + C |
| Rj: | ... |
| Rk: | D = E + A |
| Rn: | ... |
Beispiele hierfür aus unserer Konstituentenstrukturregelmenge wären die Regeln 1 (für Ri) und 8 (für Rk), 1 und 2, 1 und 20, jedesmal mit Rekursion über S. Wir haben hier eine Formalisierung der Tatsache, daß man einem Nebensatz wieder einen Nebensatz unterordnen kann, und diesem wieder einen usw. nach Belieben.
Die Rekursivität im Regelapparat ist die wichtigste Voraussetzung für zwei wesentliche Eigenschaften der mit seiner Hilfe ableitbaren syntaktischen Strukturen:
Beides spiegelt wesentliche Eigenschaften menschlicher Sprache.
Zum Schluß noch zur Veranschaulichung die Konstituentenstruktur eines komplizierteren Satzes (die Wortart N unter der syntaktischen Kategorie Nom hat man sich zu ergänzen):
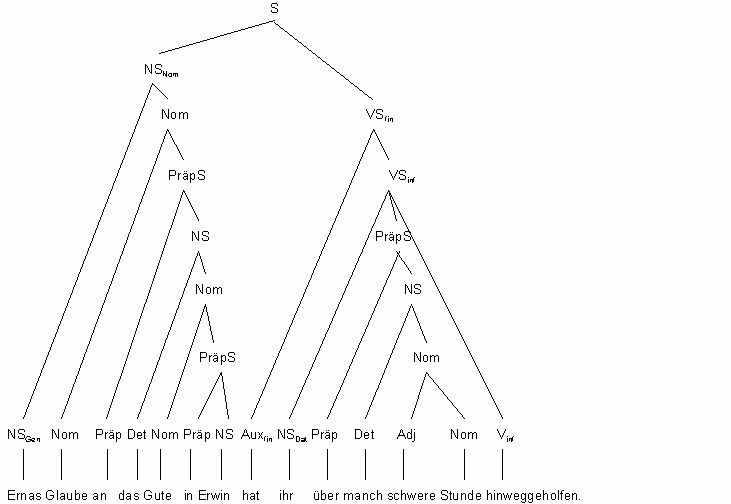
Hier sind einige Konstruktionen enthalten, die bisher nicht eingeführt wurden:
| 1. | Koordinative und subordinative Konjunktionen |
1 Dies ist ein gleichzeitig präziser, aber sehr strenger und deshalb nur selten anwendbarer Begriff von Endozentrizität, weil Rekursion in natürlichen Sprachen fast immer beschränkt ist. Z.B. ist man in B2.a schon am Ende der Rekursion; und auch B2.b ist nicht leicht zu erweitern.